#BFS Undirected Graph

[codingprolab]

CSCI 570 - HW 1

1. Arrange the following functions in increasing order of growth rate with g(n) following f(n) in your list if and only if f(n) = O(g(n)) 2 log 𝑛 , (√2) log 𝑛 , 𝑛 (log 𝑛) 3 , 2 √2 log 𝑛 , 2 2 𝑛 , 𝑛 log 𝑛 , 2 𝑛 2 2. Give a linear time algorithm based on BFS to detect whether a given undirected graph contains a cycle. If the graph contains a cycle, then your algorithm should output one. It…

[programmingandengineering]

Homework 4: Graph Algorithms: Part I

Problem 1: Graph Traversal 50 points Demonstrate both breadth-first search (BFS) and depth-first search (DFS) algorithms (with v1 as the start node) on the unweighted, undirected graph shown in Figure 1. Clearly show how each node-attribute (including frontier) changes in each iteration in both the algorithms. (20 points) Implement both BFS and DFS algorithms in Python using a graph class based…

[nullset2]

Minimum Spanning Tree -- Connect Islands with Minimum Bridges Problem

Certain problems in Computer Science can be solved with a Minimum Spanning Tree. A minimum spanning tree is a tree derived from a weighted, undirected graph, which connects all of the nodes in that graph using the least sum of weights possible.

Prim's algorithm works in a greedy manner, producing an MST for a graph by comparing distances in a BFS manner and picking the smallest one at every step of traversal.

It works by producing an adjacency matrix to represent a graph and the distances between every node (necessarily, a graph with a "cut" in the middle; think of it as an identity matrix, but with zeroes in the main diagonal rather than ones, and symmetrical values populated otherwise). This matrix usually looks like this:

[0.0, 1.0, 6.0, 3.0, 5.0, 7.0, 8.0, 9.0] [1.0, 0.0, 5.0, 2.0, 4.0, 6.0, 7.0, 8.0] [6.0, 5.0, 0.0, 5.0, 3.0, 1.0, 4.0, 3.0] [3.0, 2.0, 5.0, 0.0, 2.0, 4.0, 5.0, 6.0] [5.0, 4.0, 3.0, 2.0, 0.0, 2.0, 3.0, 4.0] [7.0, 6.0, 1.0, 4.0, 2.0, 0.0, 3.0, 2.0] [8.0, 7.0, 4.0, 5.0, 3.0, 3.0, 0.0, 1.0] [9.0, 8.0, 3.0, 6.0, 4.0, 2.0, 1.0, 0.0]

The distances used can be Pythagorean distances or Manhattan distances (sum of absolute values of differences between coordinates).

Then, you build THREE auxiliary arrays:

One to represent the parents of every node of the adjacency matrix.

One to represent the weights connecting the final MST, which we will call the "key" row.

One to mark a given node in the MST as visited.

Then, these are the instructions:

Start from node 0; mark as visited and its weight as 0.

Mark its parent as NULL (-1 in this case).

Make a comparison of all of the weights towards the nodes it's connected to. Take the smallest one, add it to the weights, move onto that node, and repeat until you exhaust all the nodes.

This is a Java implementation, using the "Islands and Bridges" problem: https://gist.github.com/nullset2/a101d39f3bdc1b3670a948e0e8416df1

Thank you!

[codezclub]

C Program for Traversing an Undirected Graph through BFS

Traversing an Undirected Graph through BFS Write a C Program for Traversing an Undirected Graph through BFS. Here’s simple C Program for Traversing an Undirected Graph through Breadth First Search(BFS). Breadth First Search (BFS) BFS is a traversing algorithm where you should start traversing from a selected node (source or starting node) and traverse the graph layerwise thus exploring the…

[abhilashkrish]

Program to find Longest Path in an Undirected Tree

import java.util.ArrayList; import java.util.Arrays; import java.util.LinkedList; import java.util.List; import java.util.Queue; /** * Program to find longest path in an unidirected tree * @author Abhilash Krishnan * @since August 07, 2018 */ class Graph { int V; List<Integer> adj[]; public Graph(int V) { this.V = V; this.adj = new ArrayList[V]; for (int i = 0; i < V; i++) this.adj[i] = new ArrayList<>(); } public void addEdge(int v, int w) { this.adj[v].add(w); this.adj[w].add(v); } public Pair bfs(int u) { int[] dist = new int[V]; Arrays.fill(dist, -1); Queue q = new LinkedList<>(); q.offer(u); dist[u] = 0; while(!q.isEmpty()) { int t = q.poll(); for (Integer v : adj[t]) { if (dist[v] == -1) { q.offer(v); dist[v] = dist[t] + 1; } } } int maxDist = 0; int nodeIdx = 0; for (int i = 0; i < V; i++) { if (dist[i] > maxDist) { maxDist = dist[i]; nodeIdx = i; } } return new Pair(nodeIdx, maxDist); } public void longestPath() { Pair t1 = bfs(0); Pair t2 = bfs(t1.v); System.out.println("Longest path is from " + t1.v + " to " + t2.v + " is " + t2.dist); } }

class Pair { int v; int dist; public Pair(int v, int dist) { this.v = v; this.dist = dist; } }

public class LongestPath { public static void main(String[] args) { Graph g = new Graph(10); g.addEdge(0, 1); g.addEdge(1, 2); g.addEdge(2, 3); g.addEdge(2, 9); g.addEdge(2, 4); g.addEdge(4, 5); g.addEdge(1, 6); g.addEdge(6, 7); g.addEdge(6, 8); g.longestPath(); } }

[whitechnoleg]

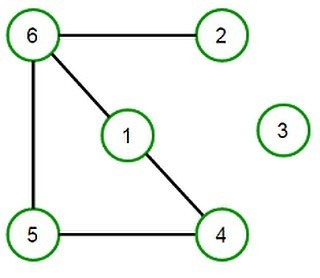
Graphs Interview Questions // techiedelight.com/graphs-interview-questions // A graph is an ordered pair G = (V, E) comprising a set V of vertices or nodes and a collection of pairs of vertices from V called edges of the graph. Graph For example for above graph, V = { 1, 2, 3, 4, 5, 6 } E = { (1, 4), (1, 6), (2, 6), (4, 5), (5, 6) } Below is the list of commonly asked graphs interview questions – Graph Implementation using STL Graph Implementation in C++ without using STL Breadth First Search (BFS) | Iterative & Recursive Implementation Depth First Search (DFS) | Iterative & Recursive Implementation Arrival and Departure Time of Vertices in DFS Types of edges involved in DFS and relation between them Bipartite Graph Minimum number of throws required to win Snake and Ladder game Topological Sorting in a DAG Transitive Closure of a Graph Check if an undirected graph contains cycle or not Total paths in given digraph from given source to destination having exactly m edges Determine if an undirected graph is a Tree (Acyclic Connected Graph) 2-Edge Connectivity in the graph 2-Vertex Connectivity in the graph Check if given digraph is a DAG (Directed Acyclic Graph) or not Disjoint-Set Data Structure (Union-Find Algorithm) Chess Knight Problem – Find Shortest path from source to destination Check if given Graph is Strongly Connected or not Check if given Graph is Strongly Connected or not using one DFS Traversal Union-Find Algorithm for Cycle Detection in undirected graph Kruskal’s Algorithm for finding Minimum Spanning Tree Single-Source Shortest Paths – Dijkstra’s Algorithm Single-Source Shortest Paths – Bellman Ford Algorithm All-Pairs Shortest Paths – Floyd Warshall Algorithm Print all k-colorable configurations of the graph (Vertex coloring of graph) Print All Hamiltonian Path present in a graph Greedy coloring of graph #graphs-interview-questions

[programmingandengineering]

Algorithms (Sec: 102) Homework 4: Graph Algorithms: Part I

In this homework, we will focus our attention to searching on graphs and finding minimum span-ning trees. Problem 1: Graph Traversal 50 points Demonstrate both breadth-first search (BFS) and depth-first search (DFS) algorithms (with v1 as the start node) on the unweighted, undirected graph shown in Figure 1. Clearly show how each node-attribute (including frontier) changes in each iteration in…